Do Deposit Matches Ever Guarantee a Profit? When is a Deal Too Good to Pass Up?
Zedekiah G. Higgs
One type of promotion that is sometimes offered by the Lottery is deposit matches, where a player's deposit is matched at some rate (e.g., 50%) up to some match limit (e.g., $100). Unlike promotional offers that provide players with free games, deposit matches usually provide players with significantly larger subsidies. For example, a promotion that provides 20 free $0.50 games provides a player with a $10 subsidy. However, a deposit match of 50% up to $100 provides the player with a $100 subsidy (the player deposits $200 into their account and receives a $100 match). Because deposit matches provide significantly larger subsidies, they allow players to spread their bets across a much larger number of games, which should theoretically make earning a positive profit on such promotions a more reliable outcome.
Can these deposit matches be relied on to earn a positive profit? How generous must the match rate be? How big must the match limit be? When is a deal too good to pass up?
To answer these questions, I build a simulation model of the Virginia Online Lottery based on the Online Instant game Jackpot Spectacular. I use the exact payoffs and win probabilities used by the Lottery. Using this model, I simulate different deposit matches, analyzing the expected profits associated with different match rates and match limits.
Simulations
In each of the following simulations, I will assume that the player maximizes the size of the subsidy received by taking full advantage of the match limit. For example, if the Lottery offers a 25% match up to a total match of $100, I will assume that the player deposits $400 of their own money, giving them $500 to play with. I will also assume that the player only plays $0.50 games (the minimum bet size in Jackpot Spectacular), maximizing the total number of games they are able to play and therefore also maximizing their chances of realizing a profit. (Playing a larger number of games reduces the variance of their final profits, reducing their potential for winning large amounts but also reducing the probability of realizing a loss.) In the example discussed, where the player ends up with a total of $500 to play games with, this means that they will play a total of 1,000 games at $0.50 per game. To earn a profit on the deposit match promotion, the player would need to earn at least $400 in winnings across their 1,000 games.
I will consider three different match offers that have previously been offered by the Lottery:
- The first match offer I will consider is a 25% match up to a total match of $100. This provides the player with a total of $500 to play with, at a cost to the player of only $400.
- The second match offer is a 50% match up to a total match of $100. This provides the player with a total of $300 to play with, at a total cost of $200. This is the most generous match rate offered by the Lottery, but it also provides the player with the smallest amount of total games.
- In the third simulation, I will again consider the 50% match offer, but I will combine all four of the 50% deposit match promotions that have been offered by the Lottery. All four times the Lottery has offered a 50% match, the match limit has always been set to $100. Thus, a player taking advantage of all four of these offers would receive a total match of $400 on a total deposit amount of $800, giving them $1,200 to play with. This is not only the most generous offer provided by the Lottery, but it also spreads the player's risk across the largest number of games. Thus, if any offer is going to guarantee a profit, this will be the one.
Simulation 1: 25% match up to $100
In this scenario, the player has $500 to play with, at a total cost to the player of $400. Therefore, the player needs to win at least $400 to earn a profit. Assuming the player bets the minimum of $0.50 on each game, this gives them a total of 1,000 plays. The following histogram shows the distribution of observed profits for 1 million simulated players playing 1,000 $0.50 games of Jackpot Spectacular.
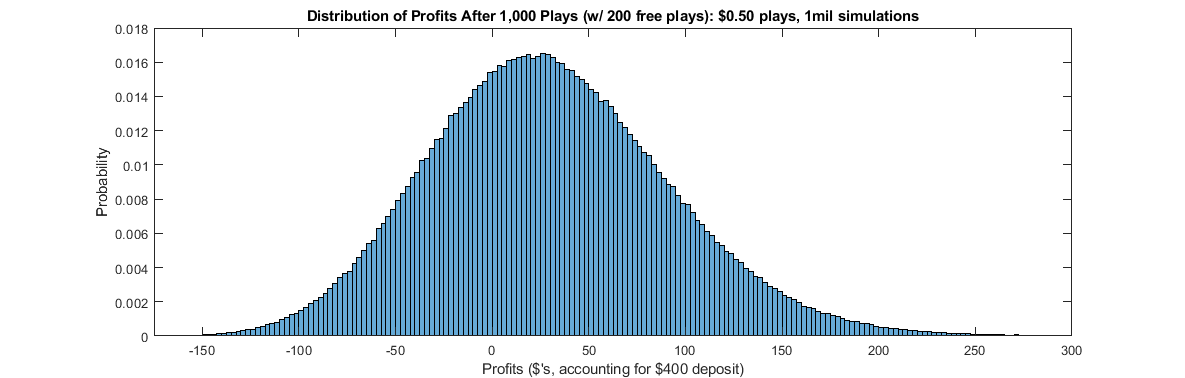
Consistent with the theoretical expected profits associated with this promotion (of $30), the average profit observed across the 1 million simulations is $30.01. However, while the distribution of profits is centered to the right of 0, it is clear that a large portion of the distribution is to the left of 0, reflecting negative profits. In fact, 32.8% of the simulated players lose money on this promotion, with 9.1% of players losing more than $50.
That being said, it is also true that 12.9% of players profit more than $100 on this promotion, so sizable profits are certainly within the realm of reality. But with nearly a third of all players losing money on this promotion, it can't be said that this offer is too good to miss.
Simulation 2: 50% match up to $100
In this scenario, the player has $300 to play with, at a total cost to the player of $200. Therefore, the player needs win at least $200 to earn a profit. Assuming the player bets the minimum of $0.50 on each game, this gives them a total of 600 plays. The following histogram shows the distribution of observed profits for 1 million simulated players playing 600 $0.50 games of Jackpot Spectacular.
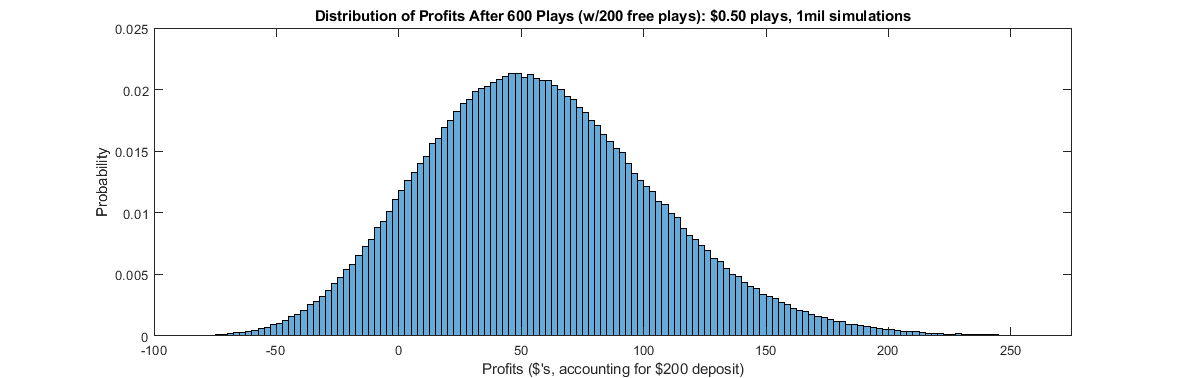
The average profit observed for this promotion is $58.01, which is very close to the theoretical expected value of $58. And it is clear that the distribution is now centered further to the right than the previous promotion. The most common outcome is now for players to earn a profit of over $50. In total, 89.5% of players earn a profit, with 54.1% profiting more than $50, 18.4% profiting more than $100, and 3.7% profiting more than $150.
Still, 10.5% of players lose money on this promotion, which is a significant portion. The number of players losing a substantial amount is low though, with only 0.4% of players losing more than $50. But with more than 1 in 10 players losing money on this promotion, it is not clear that it should be considered too good to pass up.
Simulation 3: 50% match up to $400
In this scenario, the player has $1,200 to play with, at a total cost to the player of $800. Therefore, the player needs win at least $800 to earn a profit. Assuming the player bets the minimum of $0.50 on each game, this gives them a total of 2,400 plays. The following histogram shows the distribution of observed profits for 1 million simulated players playing 2,400 $0.50 games of Jackpot Spectacular.
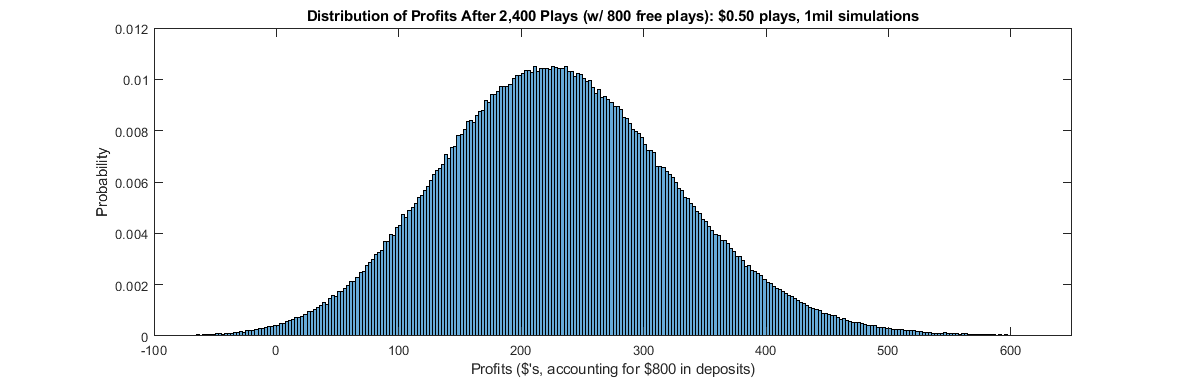
If ever there was a deal worth taking, this is it. The distribution of profits is centered well to the right of 0. The average profit earned is $231.99 (which is very close to the theoretical expected value of $232). More than 99.5% of players earn a profit, with more than half of players earning a profit greater than $228. 92% of players earn profits greater than $100, 23.1% earn profits greater than $300, and 4.6% earn profits greater than $400.
Players now have less than a 0.5% chance of losing money, with only a .06% chance of losing more than $50 (although one of the 1 million simulated players managed to lose $153.10). Indeed, players have a greater chance of profiting more than $500 (0.6%) than they do of losing any amount of money (0.5%). This demonstrates the extent to which increasing the number of draws reduces the variance and lowers risk. While a single 50% deposit match of up to $100 (Simulation 2) still gives a more than 1 in 10 chance of losing money, by combining all four of the 50% deposit matches offered by the Lottery a player is able to give themselves a greater than 99.5% chance of earning a profit.
While nothing is ever guaranteed and there is always some amount of risk involved, combining the four 50% match promotions offered by the Lottery may indeed meet the threshold of what should be considered a deal "too good to pass up."