An Introduction to How the Online Lottery Works
Zedekiah G. Higgs
This is the first part of a blog post that was originally posted to Reddit.
In what follows, I provide some background information about how the Online Lottery works and the payoff probabilities associated with the Online Instant games. The description is written in the context of promotions offered by the Lottery, which are special deals the Lottery frequently offers in which players can receive free games. Players often find that they earn very little money from the promotional offers, leading many of them to suspect that the games are rigged. This introduction to the lottery is the first part in a series of posts in which I attempt to explain why players would observe frequent losses on these promotions despite the odds technically being in their favor.
How the Online Lottery Works
When I refer to the Online Lottery, I am referring specifically to the Online Instant games. These games are essentially online slot machines. You click a button and the computer randomly determines an outcome. To make the discussion more concrete, throughout this post I am going to discuss the game Jackpot Spectacular. All of the Online Instant games work in essentially the same way, really only differing in their presentation (e.g., the graphics, sounds, etc.).
For Jackpot Spectacular, there are a total of 2 million "tickets". Each ticket corresponds to a payoff. Each time you press the play button, the computer randomly selects one of these tickets, and you then win the payoff associated with the selected ticket. The process is very similar to scratch off tickets: each time you press the play button, you are effectively purchasing a virtual scratch off. Very few of the scratch offs have large prizes, some have small prizes, and the vast majority have no prize. Unlike buying a scratch off in the store, however, each time you play an Online Instant game, the ticket you purchase gets put back into the pile of tickets, so there's some chance you'll end up buying the same ticket more than once.
The payoff associated with each ticket is expressed as a multiple of the amount you bid. In Jackpot Spectacular the possible payoffs range from 0.1x your bid amount to 1,000x your bid amount. (I am ignoring the rolling jackpots, which aren't tied to your bid size.) For example, if you bid $0.50 and draw a ticket with a 2x payoff, your total prize would be $1 (2 x $0.50 = $1). If you bid $10 and draw a ticket with a 0.2x payoff, your total prize would be $2 (0.2 x $10 = $2). The amount you bid scales your prize amounts, but the payoff associated with each ticket always remains the same, regardless of how much you bid.
The number of tickets providing each payoff determines the overall odds in a game. For example, Jackpot Spectacular has 68,120 tickets that provide a payoff of 0.1x, and there is only 1 ticket that provides a payoff of 1,000x. That means that you have a 68,120/2,000,000 = 3.41% chance of drawing a ticket with a 0.1x payoff and a 1/2,000,000 = 0.00005% chance of drawing the ticket with the 1,000x payoff. We should also keep in mind that 1,499,337 of the tickets provide no payoff at all. That is, you have a 1,499,337/2,000,000 = 74.97% chance of drawing a ticket that pays nothing.
The probabilities of drawing the different tickets in Jackpot Spectacular are provided by the Virginia Lottery here: Game Rules (valottery.com). Based on their reported probabilities, the Virginia Lottery is actually pretty generous -- not including the rolling jackpots, Jackpot Spectacular has a RTP of 0.86, meaning that 86% of the money bet in the game gets returned to players. Including the rolling jackpots, the RTP is 0.9. I believe this is significantly higher than the RTP you would get from slot machines at any casino. The reason they are able to offer such generous RTP on their online games is the reduction in overhead costs. Unlike a casino that needs a building with physical slot machines, the Online Lottery just needs to maintain its website.
The RTP also tells us how much a player can expect to win over time. At an RTP of 0.86, a player can expect to win $0.86 for ever $1 they bet. We can use this figure to give us a sense of whether or not a given promotion is worth taking. If the Lottery offers 20 free $0.50 plays of Jackpot Spectacular with a $10 deposit, this means that a $10 deposit gives the player a total of $20 in bets ($10 from the deposit and an additional $10 in free games). At an RTP of 0.86, players can expect to win $17.20 on $20 of bets. Since the player only had to deposit $10, they can expect a profit of $7.20. Thus, the odds are in the player's favor.
Notice, however, that I keep saying the player can expect to win money, not that they should expect to win money. This is because the RTP shows how much will be returned to players on average over a large number of plays. What number of plays qualifies as large? Probably much more than you think. And certainly much more than you will end up playing as part of the promotion. Even if you maximize your number of plays by always betting the minimum amount of $0.50 (which is the optimal strategy to use if you are trying to maximize the probability of earning a profit), you will still only play a total of 40 games in the example provided. This is nowhere near enough plays to guarantee a RTP anywhere close to the "expected" value of 0.86. Why? Because the distribution of payoffs is extremely skewed.
To demonstrate just how skewed the distributions of payoffs are in the Online Instant games, below I present a histogram of payoffs for Jackpot Spectacular.
The x-axis shows the payoff as a multiple of the amount bet (e.g., 0.1x, 0.2x, ... , 1000x). It ranges from 0 all the way to 1,000 because the top payoff you can receive is 1,000x. The y-axis shows the probability of receiving each payoff.
If you're like me, you probably don't see much. It looks like there's nothing in the graph. That's because the probability of receiving a payoff greater than 10x is tiny, so nothing shows up on the graph. If you look carefully at the bottom left corner, you can see some stuff. That's because the vast majority of payoffs are near 0.
To help you see what's going on, below I repeat the graph, but this time I ignore any payoffs greater than 25x.
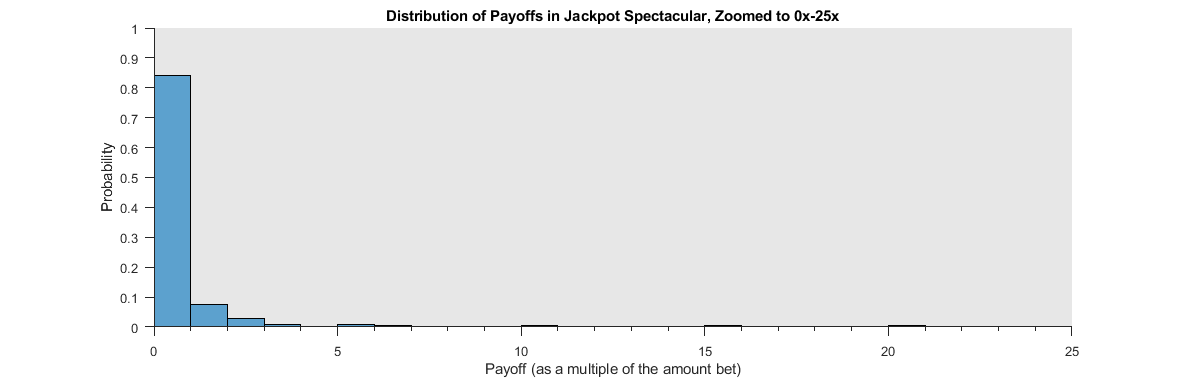
The first bar shows the probability of receiving a payoff between 0x and 1x. More than 84% of the tickets provide a payoff that is less than 1x. That is, on more than 84% of plays you will lose money, bringing in less than the amount you bet. If you include tickets with payoffs of 1x in the category of "losing tickets", then losing tickets account for a whopping 89% of all of the tickets. On each play, you only have an 11% chance of winning more than you bet, and even when you do draw a winning ticket the vast majority of the time it won't be for a large payoff.
Of course, if you're trying to earn a profit from a promotion, drawing tickets that pay less than 1x are still helpful: you're simply trying to convert your spins into the largest payoff possible so you can withdraw the money from your account. But the payoff distribution still isn't great for you, because most of the losing tickets actually pay 0. To see this, I zoom in even more and change the bin width to 0.1 so payoffs of 0 become their own bar.
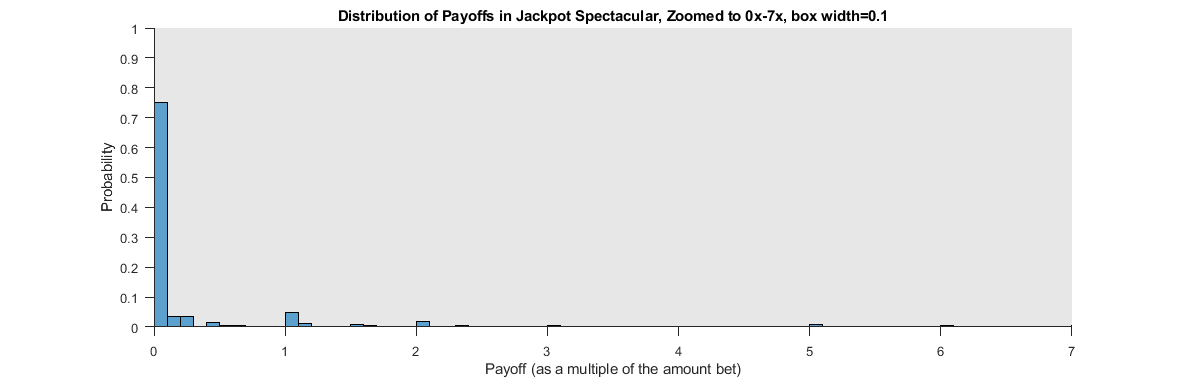
The first bar shows the probability of drawing a ticket that pays nothing. You have about a 75% chance of winning nothing on any given play. The second most likely payoff is 1x. Higher payoffs raise the average and increase the RTP, but they become increasingly unlikely. Over a relatively small number of plays -- such as the number of games you would typically play as a result of a promotion -- there is a good chance you will never hit a payoff greater than 5x. This will be demonstrated in the simulations I will run in future posts on this subject, in which I will calculate how often one should expect to profit from various promotions offered by the Lottery.