Are the Virginia Online Lottery Promotions Rigged? An Analysis of Expected Earnings Using Simulation Methods
Zedekiah G. Higgs
This is the second part of a blog post that was originally posted to Reddit.
The Virginia Online Lottery often offers promotions to incentivize players to deposit money and play games. For example, the Lottery might offer 20 free plays of a particular Online Instant game at a given price level (e.g., $0.50 plays of Jackpot Spectacular) to any player who deposits at least $10 into their account. These promotions can shift the odds into the player's favor, so that in expectation a player can earn a small profit.
However, even in cases where the promotion is very generous -- such as a 100% match -- it is not uncommon for players to report losing money. Moreover, many players find that they actually lose money on such promotions on a regular basis. If the odds are truly in the player's favor, then why are losses so often realized? Obviously nothing is ever guaranteed, but when a player repeatedly loses money on promotions that ostensibly should provide a significant statistical edge, it is understandable that they would question the integrity of the Lottery. After all, why would the Lottery want to provide a promotion that will lose them money? If a player is using promotions to consistently beat the house, it would make sense that the Lottery would attempt to find ways to get their money back.
In this post, I detail how the Online Lottery works and analyze how often one should expect to earn a profit when taking advantage of promotions. I build a simulation model of the Online Instant game Jackpot Spectacular, using the actual payoff probabilities used by the Virginia Lottery. I then use the model to simulate the outcomes of various promotions and answer the following questions: (1) How often should one expect to earn a profit from a promotion? (2) At what point are a player's earnings suspiciously low? And (3) Do we have reason to believe that the Virginia Online Lottery is rigged or that it targets accounts that only respond to promotional offers?
In what follows, I begin by briefly discussing why simulation is needed to understand the likelihood of earning a profit on a given promotion. I then consider two common promotional offers and discuss how often you should expect to earn money on them.
Why This Problem Requires Simulation
If we want to know the probability of losing money on a given promotion, one might assume that deriving an analytical solution would be optimal. The issue is that the state space is far too large. There are more than 100 different possible payoffs (or outcomes) that can occur for any given play. Thus, calculating all of the different final profits a player could earn as a result of playing 40 games of Jackpot Spectacular would require considering more than 100^40 different possible states. That's way too many.
So, instead of trying to identify every possible state, we can just play 40 games of Jackpot Spectacular over and over again, keeping track of how much we profit each time we do so. If we do this enough times, we will get a good sense of the distribution of expected profits. It won't be exactly perfect, but the more simulations we run the closer it will get. (I am going to use 1 million simulations.)
One way to think of this process is that we are having 1 million people play 40 games of Jackpot Spectacular to see how much they win. While we won't observe every outcome that could possibly occur, we will see enough outcomes to get a good sense of the distribution.
The simulation is exactly like playing the real game. There are two million possible tickets, with the payoffs associated with each ticket corresponding to the exact values used by the Virginia Lottery. In each play, the computer randomly selects one of the tickets. Unlike the real game, though, the simulation can go through the plays at a much faster pace. And, more importantly, the simulation is free.
Simulations
Scenario 1: The first scenario I simulate is a promotion where the Lottery offers 20 free $0.50 plays of Jackpot Spectacular with a $10 deposit. This is equivalent to a 100% match, which is the most generous promotion I have seen offered. I assume that the player plays all of their 20 free games and then continues to play an additional 20 games, still at $0.50 a game, to convert their $10 deposit into winnings that they can withdraw. So the player will play a total of 40 games, all at $0.50 per game. This is the optimal strategy for a player who wants to maximize the probability of earning a profit on the promotion.
To earn a profit, the player must win more than $10 over their 40 plays. If they win less than $10, then they will fail to recoup their $10 deposit and will have lost money on the promotion. As stated before, their expected winnings over 40 games is $17.20, corresponding to a $7.20 profit. But how much variability should they expect in their total winnings over 40 games?
Below I present a histogram of the total profits for 1 million simulated players.
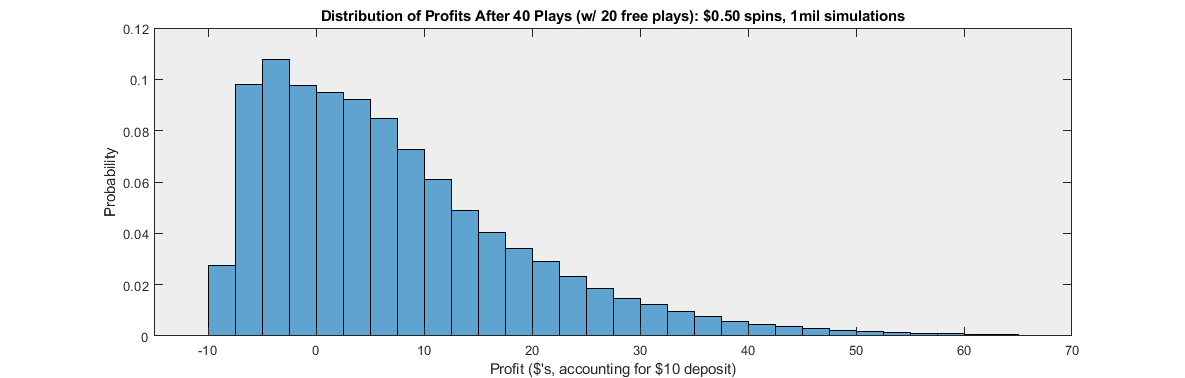
Each bar has a width of $2.50. That is, the first bar shows the probability of earning a profit greater than or equal to -$10 and strictly less than -$7.50, the second bar shows the probability of earning a profit greater than or equal to -$7.50 and strictly less than -$5, etc. I have limited the x-axis to be less than 70 because higher profit outcomes are so rare that they can't be seen on the graph. (The highest profit earned by one of the one million simulated players was $528.05.)
Note that even with this generous promotion of a 100% match, the most common outcome is for players to lose between $2.50 and $5. Overall, more than 33% of players lose money on this promotion!
What's the average profit earned by players? In this simulation, the average profit comes out to $7.21, which is very close to the theoretically expected value of $7.20. So, it's true that the Lottery loses money on this promotion, but it's also true that many players will also lose money.
The first bar shows the probability of earning a profit between -$10 and -$7.50. These players end up winning less than $2.50 over 40 plays. This may sound almost impossible, but we see that actually 2.7% of players will end up in this category.
Scenario 2: The second scenario I simulate is one where the Lottery offers 10 free $0.50 plays when a player deposits $10. This is equivalent to a 50% match on the player's deposit (assuming they deposit the minimum amount of $10). This is less generous than Scenario 1, but it still shifts the odds in the player's favor.
Combining the free games with the $10 deposit, players get to gamble a total of $15 at a cost of only $10. At the RTP rate of 0.86, players can expect to win around $12.90, bringing in an expected profit of $2.90 from the promotion. This obviously isn't as generous as the 100% match in Scenario 1, but on average players should still benefit from the promotion.
However, just like we saw in Scenario 1, the simulation demonstrates that the average outcome is very different from what any single player can expect to experience.
Below is a histogram of the profits earned by 1 million simulated players responding to the promotion. As before, I assume that all players play all of their free games and then continue playing $0.50 games until they spend their entire deposit, so that all players play a total of 30 games.
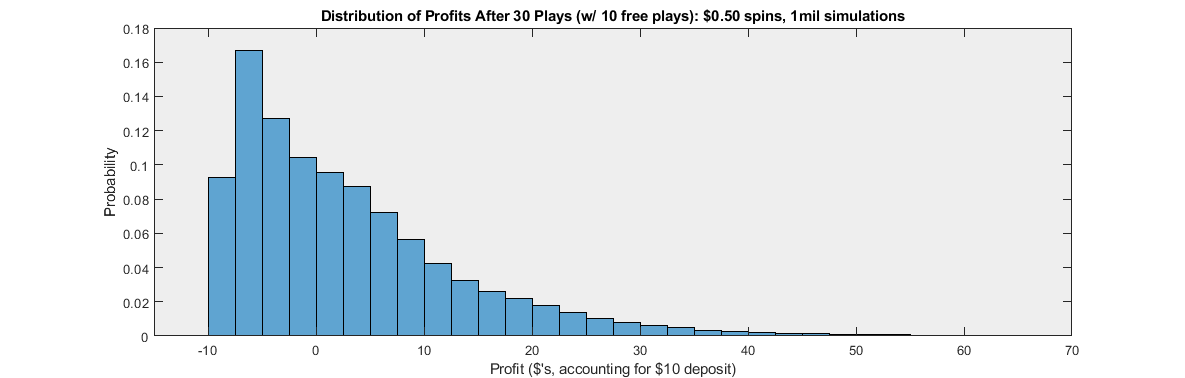
As before, each bar has a width of $2.50 and the x-axis is capped at $70 to make things easier to see. (The highest profit earned by any of the one million simulated players is $524.15.)
With this less generous offer of a 50% match, it is now much more likely that a player will lose money. Less than 51% of players earn a positive profit on the promotion, with more than 49% losing money. The most common outcome for players is to lose between $5 and $7.50. That is, the most common outcome over 30 plays of Jackpot Spectacular is for a player to win a measly $2.50 to $5.
Furthermore, 9.3% of players now lose between $7.50 and $10. That is, almost 1 in 10 players will win less than $2.50 over 30 plays. (That's a lot of really upset people.) About 1 in 6,000 players are so unlucky they never win a single cent over all 30 games -- they lose 30 times in a row. In fact, you're about 14 times more likely to win nothing across all 30 games than you are to win the top non-jackpot prize of 1000x in any of your 30 plays (which would be a payoff of $500 for a $0.50 spin).
Conclusion
The simulations make it clear that promotional offers that tip the odds in a player's favor are no guarantee that the player will earn a profit, even if players earn profits on average. Due to the high variance of the payoff distribution and the relatively low number of games a player will play as part of any given promotion (typically 40 or fewer plays), a high percentage of players will lose money despite the odds technically being in their favor with respect to expected (i.e., average) payoffs.
For a 100% match with a $10 deposit, more than 33% of players will lose money, failing to recoup the cost of the $10 deposit. For a 50% match with a $10 deposit, more than 49% of players will lose money. Clearly, earning a profit is far from guaranteed.
Moreover, a significant number of players will experience very poor outcomes. For a 50% match with a $10 deposit, nearly 1 in 10 players (9.3%) will win a total amount less than $2.50 across all of their spins, resulting in a net loss of over $7.50 from the promotion. Even for the more generous promotion of a 100% match on a $10 deposit, 2.7% of players will still win a total amount less than $2.50.
While repeated poor outcomes over multiple promotions may instinctively feel too improbable to be random, they are in fact not that unlikely. This is especially true considering that many promotions are not as generous as the ones considered here (e.g., 20 free games of $0.20 spins, which is only a 40% match).
Overall, while it is true that the Lottery technically has an incentive to take measures to prevent players from "gaming the system" by only playing when promotions are offered, poor outcomes among individual players provides little evidence of any sort of interference. Furthermore, the losses experienced by the Lottery resulting from the small group of players who only play when there is a promotion average out to only a few dollars per player. This cost is insignificant to the Lottery as a whole, and is likely less than what it would cost to rig the games to take the money back from those players. Plus, the potential reputational cost associated with attempting to rig the lottery would be huge. Given how forthright the Lottery is with posting the exact odds for each Online Instant game, combined with the results of the simulations I have presented here, I personally don't believe there is any reason to suspect any foul play.